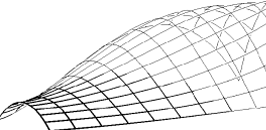
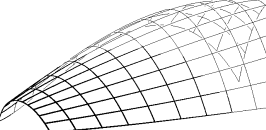
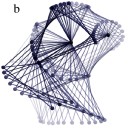
A matching algorithm is introduced to generate an improve metamorphosis of freeform curves. The left shows direct convex combination while the right shows the result of applying the matching algorithm. Note the back and tail of the Oryx.
This works experiments with a three dimensional interactive sculpting paradigm that employs a collection of scalar uniform trivariate B-spline functions. The sculpted object is evaluated as the zero set of the sum of the collection of the trivariate functions defined over a three dimensional working space, resulting in multi-resolution control capabilities. The continuity of the sculpted object is governed by the continuity of the trivariates. The manipulation of the objects is conducted by modifying the scalar control coefficients of the meshes of the participating trivariates. Real time visualization is achieved by incrementally computing a polygonal approximation via the Marching Cubes algorithm. The exploitation of trivariates in this context benefits from the different properties of the B-spline's representation such as subdivision, refinement and convex hull containment.
The image on the left is a result of modeling a kids' slide in this system while etching the "slide" at a higher resolution.
The image on the right is the result of employing a 3D scanner data to reconstruct the model using trivariates while further manipulations is conducted (removal of the pupils) in the modeling environment.
With the increasing complexity of photo-realistic scenes, the question of building and placing objects in three-dimensional scenes is becoming ever more difficult. While the question of placement of rigid objects has captured the attention of researchers in the past, this work presents an intuitive and interactive scheme to properly place deformable objects with the aid of free-form deformation tools. The presented scheme can also be used to animate the locomotion of non-rigid objects, most noticeably animals, and adapt the motion to arbitrary terrain. The automatic construction of our free-form deformation tool is completely hidden from the end user, and hence, circumvents the difficulties typically faced in manipulating these deformation functions. Further, a precise bound on the error that is introduced by applying free-form deformations to polygonal models is presented, along with an almost-optimal adaptive refinement algorithm to achieve certain accuracy in the mapping.
Tensor product surfaces are now widely used in application areas from industrial design to computer animation. Yet, the quest for more effective design methods continues. This work considered a new approach to the design of free form surfaces using global second order differential geometric constraints defined over the entire domain of the surface or a prescribed subset of it. Three cases of convexity preservation, developability preservation, and minimal surfaces have been considered. The image on the left shows a portion of a cockpit surface automatically shaped into the right image, preserving convexity. Created with the aid of the IRIT modeling environment.
The use of blending and filleting operations in solid modeling and computer-aided geometric design is well established. The question of filling a gap between two (or more) surface boundaries or rounding a sharp edge has been extensively investigated. The vast majority of the prior work on blending and filleting concentrated on a wide variety of fitting schemes as well as attempts to establish and guarantee better continuity conditions. This work extends the notion of filleting and blending modeling tools and elevates them into shaping operations that are either functional or ornamental in nature. The extended shaping operations can be conducted between two boundaries of two adjacent surfaces, much like traditional blending or filleting methods. Furthermore, the presented extended forms can also be applied to the interior of a single surface, guided by arbitrary parametric curves in the domain of the patch.
This model of the B58 plane was modeled using the IRIT modeling environment and raytraced using the rayshade ray tracer.
Another high quality scene that was modeled using the IRIT modeling environment and raytraced using the rayshade ray tracer. This scene as well as the B58 above were constructed using various freeform surface modeling tools such as ruled surface (wings of B58), surface of revolution (the table and dishes), sweep (the cushion and base of chairs), and skinning (the fuselage of the B58). Similar geometries such as the engines of the B58 or the chair were instantiated several times using rigid motion transformations
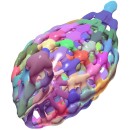
We introduce a modeling constructor for micro-structures and porous
geometry via curve-trivariate, surface-trivariate and
trivariate-trivariate function (symbolic) compositions. By using 1-,
2- and 3-manifold based tiles and paving them multiple times inside
the domain of a 3-manifold deforming trivariate function, smooth,
precise and watertight, yet general, porous/micro-structure geometry
might be constructed, via composition. The tiles are demonstrated to
be either polygonal meshes, (a set of) Bezier or B-spline curves, (a
set of) Bezier or B-spline (trimmed) surfaces, (a set of) Bezier or
B-spline (trimmed) trivariates or any combination thereof, whereas the
3-manifold deforming function is either a Bezier or a B-spline
trivariate.
We briefly lay down the theoretical foundations, only to demonstrate the
power of this modeling constructor in practice, and also present a few 3D
printed tangible examples. We then discuss these results and conclude
with some future directions and limitations.
Sampled micro-structures, including of the knot model shown on the right, in obj and iges formats, can be found here
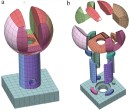
With the recent development of Iso-geometric Analysis (IGA) (Cottrell et al., 2009) and advanced manufacturing technologies employing heterogeneous materials, such as additive manufacturing (AM) of functionally graded material, there is a growing emerging need for a full volumetric representation of 3D objects, that prescribes the interior of the object in addition to its boundaries. In this paper, we propose a volumetric representation (V-rep) for geometric modeling that is based on trimmed B-spline trivariates and introduce its supporting volumetric modeling framework. The framework includes various volumetric model (V-model) construction methods from basic non-singular volumetric primitives to high level constructors, as well as Boolean operationsí support for V-models. A V-model is decomposed into and defined by a complex of volumetric cells (V-cells), each of which can also represent a variety of additional varying fields over it, and hence over the entire V-model. With these capabilities, the proposed framework is able of supporting volumetric IGA needs as well as represent and manage heterogeneous materials for AM. Further, this framework is also a seamless extension to existing boundary representations (B-reps) common in all contemporary geometric modeling systems, and allows a simple migration of existing Brep data, tools and algorithms. Examples of volumetric models constructed using the proposed framework are presented.
This paper proposes new methods and algorithms for the construction of micro-structures that leads to a high degree of precision and water-tight models. That proposed approach involves the tiling of the domain of a deformation map using copies of a tile. The resulting tiling is functionally composed into the deformation map to obtain freeform micro-structures. Such a decoupling of the micro and macro structures allows a simplified control over design parameters. Herein, we present several extensions to this micro-structure construction scheme, comprising bivariate and trivariate tiles, implicit and parametric, including with potential discontinuities. We present support for fractal-like micro-structures, with self-similarity, allow the encoding of volumetric properties and hence heterogeneity, support for shelling and capping boundary operations, random tiling and bifurcation tiling, and support for degree reduction of the result. We verify the robustness of our approach by subjecting some of our heterogeneous micro-structures to isogeometric analysis. Finally, a variety of results from an implementation of our algorithms are also presented.
Piecewise polynomial constraint systems are common in numerous problems in computational geometry, such as constraint programming, modeling, and kinematics. We propose a framework that is capable of decomposing, and efficiently solving a wide variety of complex piecewise polynomial constraint systems, that include both zero constraints and inequality constraints, with zero-dimensional or univariate solution spaces. Our framework combines a subdivision-based polynomial solver with a decomposition algorithm in order to handle large and complex systems. We demonstrate the capabilities of our framework on several types of problems and show its performance improvement over a state-of-the-art solver.
Trimmed \Bspline{} surfaces are common in the geometric computer aided design (CAD) community due to their capability to represent complex shapes that can not be modeled with ease using tensor product \Bspline{} and \NURB{} surfaces. However, in many cases, handling trimmed-surfaces is far more complex than tensor-product (non-trimmed) surfaces. Many algorithms that operate on tensor-product surfaces, such as algorithms toward rendering, analysis and manufacturing, need to be specially adapted to consider the trimming domains. Frequently, these special adaptations result in lack of accuracy and elevated complexity. In this paper, we present an algorithm for converting general trimmed surfaces into a set of tensor-product (typically \Bspline{}) surfaces. We focus on two algorithms to divide the parametric space of the trimmed surface into four-sided quadrilaterals with freeform curved boundaries, which is the first step of the algorithm. Then, the quadrilaterals are parameterized as planar parametric patches, only to be lifted to the Euclidean space using a surface-surface composition, resulting in tensor product surfaces that precisely tile the input trimmed surface in Euclidean space. The algorithm is robust and precise. We show that we can handle complex, industrial level, objects, with numerous high orders and rational surfaces and trimming curves. Finally, the algorithm provides user control on some properties of the generated tensor-product surfaces.
Since the first publications on composition of splines~\cite{DeRose1993,symbolic_bspline_ops_elber1992}, it was clear that the composition, T(S), of a tensor product \Bspline{} function S with another \Bspline{} function T is no longer a tensor product \Bspline{} if S crosses a knot line in the domain of T. The reason can be easily explained for the fact that the new function T(S) has a finite continuity that is governed by the knot line of T that is not, in general, an iso-parametric direction of the resulting composition T(S). In this work, we propose two approaches to circumvent this long standing difficulty and reconstruct precise representations for T(S) that are either tensor products or trimmed geometry. We focus our discussion on surface-trivariate compositions, T(S), while we present examples and results, for both reconstruction approaches, for microstructure surfaces and trivariates embedded in surface and trivariate deformation functions.